Speculative Fiction Writers Guide to War, part 17: War Costs: Food per Fighter
Travis P here. Since Travis C did an excellent job giving an overview of the costs of war essential to providing for a military, I think it’s time to give the math-lovers out there some hard data that can actually be used in formulas to make generate specific data on what an army might need, starting with the most basic possible cost of war–the cost of putting food in the bellies of war fighters. Which starts with a look at how much food per day a war fighter needs. You as a writer may never need these resources, but if you ever do, we’ve compiled some data to indicate just how much food it takes to keep an army fighting in the field. (Note this post wound up being longer than normal, but I’ve used bold text to highlight key ideas for those who will skim this article rather than read every word.)
The place to start with this kind of analysis is based on historical data, what real world armies have already done and then to expand from there to discussion of imaginary armies composed of fighters who are literally not of this world. We’ll also in future installments cover some of the issues regarding what it takes for a nation to produce sufficient food, which relates to the transportation of food and other supplies. Which will segue nicely into future posts that will provide some formulas that relate to transportation (and more).
How Much Food Per Human War Fighter
The first numerical summary I’ll share here of how much food an army needed per day was from the records of the Colonial Army prior to US independence from Great Britain (1775). What they listed as their daily needs surprised me in its last item (source, a US Army Quartermaster piece entitled The History of Rations):

Credit: Savoring the Past.net
l6 oz. beef (probably salted)(about 1100 calories) (193 grams)
18 oz. flour (about 900 calories) (510 grams)
1.4 oz. rice (about 150 calories) (40 grams)
16 oz. milk (about 300 calories) (454 grams)
1 qt. spruce beer (about 450 calories) (907 grams/ml)
Total: roughly 3,000 calories per day (caloric value of food varies according to exact type, which is partially unknown), weighing 5 pounds 10 ounces or 2.56 kilograms. While the beef, flour, rice, and beer could be stored over a long period of time, the milk would have to have come from fresh-milked cows, due to a lack of refrigeration at that time.
Note that the members of the Colonial Army often enough did not receive this much food. But this list, even though a bit idealized, took into account the higher calories a person needs when marching from battlefield to battlefield, a number significantly higher than the roughly 2000 calories per person that’s considered an ordinary caloric intake in our time. The variety of food reflects a rudimentary understanding of nutrition–spruce beer, made from a brew that included fresh spruce tree needles, was intended to prevent scurvy (which it did because the needles added a certain amount of Vitamin C to the beer). (Spruce beer was the surprise item on this list, because I’d never heard of it before!)
Note also that the average size of a Colonial soldier was less than a modern American–and smaller people on average require fewer calories. A modern US Army MRE (Meal Ready to Eat) has approximately 1250 calories, so three per day would equal 3750 calories, which is a more appropriate calorie count for larger people. More on MREs and calories per size a bit later.
To further illustrate the issue of people needing a different number of calories in accordance with the work they perform, let’s look at the German rationing system for food during WWII (cited in the Wikipedia article Garrison Ration).
The Germans used 4 different levels of allotments for food, based on how hard they perceived a person was working and how much food they needed. Note this system was based on a number of scientific measurements. The food supplied was specific to what Germany was able to produce, but it covered all nutritional needs for their military well–even at the lowest calorie level, these were not starvation rations (sadly the Germans applied starvation rations elsewhere).
Ration I (Verpflegungssatz I) was for troops committed to combat, for those that are recuperating from combat, and for troops stationed in Norway north of 66° N. Latitude (because living in extreme cold requires a higher caloric intake).
Ration II (Verpflegungssatz II) was for occupation and line-of-communication troops.
Ration III (Verpflegungssatz III) was for garrison troops within Germany.
Ration IV (Verpflegungssatz IV) went to military office workers and nurses within Germany.
| Food Item | Ration I | Ration II | Ration III | Ration IV |
| Rye bread | 700g (1.54 lb)
1590 calories |
700g (1.54 lb)
1590 cal |
700g (1.54 lb)
1590 cal |
600g (1.32 lb)
1360 cal |
| Fresh meat with bones | 136g (4.8 oz)
About 250 cal |
107g (3.7 oz)
About 200 cal |
90g (3.17 oz)
About 170 cal |
56g (2 oz)
About 100 cal |
| Soybean flour | 7g (0.24 oz)
280 cal |
7g (0.24 oz)
280 cal |
7g (0.24 oz)
280 cal |
7g (0.24 oz)
280 cal |
| Headless fish | 30g (1 oz)
About 40 cal |
30g (1 oz)
About 40 cal |
30g (1 oz)
About 40 cal |
30g (1 oz)
About 40 cal |
| Fresh vegetables and fruits | 250g (8.8 oz)
About 100 cal |
250g (8.8 oz)
About 100 cal |
250g (8.8 oz)
About 100 cal |
250g (8.8 oz)
About 100 cal |
| Potatoes | 320g (11.29 oz)
150 cal |
320g (11.29 oz)
150 cal |
320g (11.29 oz)
150 cal |
320g (11.29 oz)
150 cal |
| Legumes | 80g (2.8 oz)
64 cal |
80g (2.8 oz)
64 cal |
80g (2.8 oz)
64 cal |
80g (2.8 oz)
64 cal |
| Pudding powder | 20g (0.70 oz)
About 470 cal |
20g (0.70 oz)
About 470 cal |
20g (0.70 oz)
About 470 cal |
20g (0.70 oz)
About 470 cal |
| Sweetened condensed skim milk | 25g (0.88 oz)
83 cal |
25g (0.88 oz)
83 cal |
25g (0.88 oz)
83 cal |
25g (0.88 oz)
83 cal |
| Salt | 15g (0.5 oz) | 15g (0.5 oz) | 15g (0.5 oz) | 15g (0.5 oz) |
| Other seasonings | 3g (0.1 oz) | 3g (0.1 oz) | 3g (0.1 oz) | 3g (0.1 oz) |
| Spices | 1g (0.03 oz) | 1g (0.03 oz) | 1g (0.03 oz) | 1g (0.03 oz) |
| Fats and bread spreads | 60g (2.11 oz)
422 cal |
50g (1.76 oz)
352 cal |
40g (1.41 oz)
282 cal |
35g (1.23 oz)
246 cal |
| Coffee | 9g (0.32 oz) | 9g (0.32 oz) | 9g (0.32 oz) | 9g (0.32 oz) |
| Sugar | 40g (1.4 oz)
135 cal |
35g (1.23 oz)
118 cal |
30g (1.05 oz)
101 cal |
30g (1.05 oz)
101 cal |
| Supplementary allowances | 2g (0.07 oz) | 2g (0.07 oz) | 2g (0.07 oz) | 2g (0.07 oz) |
| Total Maximum Ration in grams / pounds | 1698 / 3.74 | 1654 / 3.64 | 1622 / 3.57 | 1483 / 3.26 |
| Total Maximum Ration in Approximate Caloric Value (Note calories are approximations due to exact foods used being unknown) |
3584
About 3600 calories |
3447
About 3450 calories |
3330
About 3300 calories |
2994
About 3000 calories |
(Note under some circumstances, such as a soldier being very large, or extreme cases of long marches, the calorie intakes listed would be insufficient–but the system did work for most people under most circumstances.)
More ancient sources that list rations are, not surprisingly, not as nutritionally balanced. According to the online source Alimentarium, during the time of the early Roman Empire, each Roman soldier was allotted 2 Roman pounds (1 pound 5 oz or 657.8 grams) per day of bread, plus an unknown amount of meat, olive oil, and sour wine. Salt and the kinds of fruits that would stave off scurvy are not included in this daily ration at all. Though we should note that Roman soldiers ate fruits when available. (Romans always ate from local cuisine in addition to what they were rationed.)
 The Romans would march with cows and wagons full of bacon, grain, olive oil, and sour wine as part of their baggage train. An individual soldier might carry some hard biscuits, bacon, and sour wine on his person, but most of the food was provided for the entire army at once, based to a large extent on what the local civilian economy supplied. Which was to a certain extent how all ancient and many medieval armies operated. Food supply was for the entire army, not really for soldiers as individuals. Without cooks (almost always civilians until WWI) to process the food, the army would go hungry.
The Romans would march with cows and wagons full of bacon, grain, olive oil, and sour wine as part of their baggage train. An individual soldier might carry some hard biscuits, bacon, and sour wine on his person, but most of the food was provided for the entire army at once, based to a large extent on what the local civilian economy supplied. Which was to a certain extent how all ancient and many medieval armies operated. Food supply was for the entire army, not really for soldiers as individuals. Without cooks (almost always civilians until WWI) to process the food, the army would go hungry.
The reason this was true was because of spoilage. Fresh food doesn’t usually keep for very long but live animals obviously don’t normally get eaten by bacteria due to their own immune systems (fresh milk will clearly not keep long, but if you keep the milk cows with you, you can provide fresh milk on a continual basis). Certain foods like grain or flour resist bacteria because they are dry. Dry cheeses also resist bacteria and have been used to supply some ancient and medieval armies (olive oil, while not dry, contains no water and as a result resists bacteria). Alcohol also resists bacteria and was for a long time in various forms part of the supply ration for many militaries (a ration of rum was common for colonial-era navies–a ration of whiskey was allotted to the men of the Lewis and Clark expedition).
Another advantage of alcohol as food supply is that some types, such as beer and wine, have water within them, which means they can help supply the body’s need for hydration. Whiskey and rum cannot do that effectively on their own, but when mixed with water, they serve as a purifier for water, since many ancient water sources were contaminated with bacteria or other microorganisms that alcohol kills. (While this article is barely touching on the issue of hydration, please note that military operations requiring a lot of marching may require on average about 6 liters, or 6 quarts, of water or other liquid containing water, per day.)
Pastoral nomad warriors of the past, who were able to sustain themselves off their herds, would simply drive the herd with them if going into a battle that would take a long time (and leave the herd in a safe place if going on a raid). Though of course the professional armies in world history have been supported by sedentary agricultural production. Since most agricultural nations have primarily produced grain (whether that be wheat, barely, oats, rice, or corn/maize) and secondarily livestock along with the fact that grain at least needs to be boiled in water if not baked into bread to be edible, while livestock needs to be slaughtered, butchered, and cooked to be edible, that meant that soldiers mostly could not carry their own food on their person. They were either dependent on what they could obtain from the civilian economy (which, especially if they were invading enemy territory, probably meant stealing from civilians) or soldiers required an entire army camp apparatus to provide their food. Or some of both.
Since it’s possible for soldiers to be cut off from the field kitchen feeding them or it may be necessary for them to spend extended periods of time away from such a kitchen in a combat operation (this can happen to sailors, too, but is not nearly as common at sea), militaries over time have worked to make rations more compact and easier to carry on a person in combat. An early step in this direction came in the late Eastern Roman Empire, a.k.a the Byzantine Empire, which eventually changed its philosophy on supply (along with the introduction of the Theme system). Each individual soldier was required to supply himself with 20 days of food, usually in the form of grain. The Byzantines carried a paximadion, a hand mill, to grind their own grain to make a rough bread that was their primary sustenance in battle, a bread the soldiers would make themselves, providing them a measure of independence in food supply that didn’t exist for most armies of their time.
It wasn’t until World War I that it became possible to feed a soldier a complete set of rations while separated from a field kitchen. That’s because of the invention of canning (“tinning” in the UK) allowed food of sufficient nutritional value to be stored in a way that would keep it safe from spoilage. World War II also used canned (tinned) foods for soldiers who could not easily be fed in field kitchens.

Freeze dried food. Credit: Backdoor survival
Post-World War II, the practice of freeze-drying food, which actually had been pioneered by the Incas in South America (circa the 1400s), provided the most compact form of food currently known. With freeze-dried food, it’s possible to carry 3000-4000 calories per day at a weight of only 1.5 to 2 pounds per day (680 – 907 grams). (Of course you still have to add water.)
While freeze-dried food is the most compact form of food in common use, many militaries have moved away from using it, because freeze-dried food isn’t particularly tasty and in wartime, the supply of water isn’t guaranteed and may have to be carried by soldiers–so you might as well include the water in the food in the first place. In fact, the infamous US Army ration of modern times, the “Meal Ready to Eat,” (MRE) is “ready” because it ISN’T freeze-dried (though some early versions of MRE’s included some freeze-dried food, none do now).
Generally, a MRE contains the following items (from GoArmy.com):

Credit: Amazon.com
-
Entree – the main course, such as spaghetti or beef stew
-
Side dish – rice, corn, fruit, or mashed potatoes, etc.
-
Cracker or bread
-
Spread – peanut butter, jelly, or cheese spread
-
Dessert – cookies or pound cakes
-
Candy – M&Ms, Skittles, or Tootsie Rolls
-
Beverages – Gatorade-like mixes, cocoa, dairy shakes, coffee, tea
-
Hot sauce or seasoning – in some MREs
-
Flameless Ration Heater – to heat the entree
-
Accessories – spoon, matches, creamer, sugar, salt, chewing gum, toilet paper, etc.
Each MRE provides an average of 1,250 calories (13 percent protein, 36 percent fat, and 51 percent carbohydrates) and one-third of the Military Recommended Daily Allowance of vitamins and minerals.
Each MRE weighs between 18 and 26 ounces depending on the specific meal (510 to 740 grams), so an entire day’s provisions would weigh between 3 pounds 6 ounces (1.53 kg) and 4 pounds 14 ounces (2.22 kg). Which is heavier than freeze-dried food, but not a great deal and they are easier to consume.
Futuristic food is not likely to get any more efficient than freeze-dried/MRE-style meals. Star Trek fans may cite the replicator at this point–which can transform energy, which in theory weighs nothing, into food. This would seem to be the ultimate way of making food lightweight, right? Of course, speculative fiction authors are of course free to invent what they want; however, you should be aware that a food replicator is an unrealistic type of technology.
Directly transferring energy into food (Star Trek replicator style) would use a lot of energy. More than you might imagine–that is, if a replicator is truly thought of as directly converting energy into food. That process would be covered by the formula E=MC^2, or to flip that around for creating mass, M=E/C^2. Since “C” is the speed of light and that’s about 300,000 kilometers per second (186,000 miles/sec) that means C^2 is “only” roughly 90,000,000,000,000,000 (9×10^16). Which means if you decide to make 1 kilogram worth of spruce beer in your replicator (because you’re curious what it would taste like) (one kilogram, by the way, is about what the US Colonial ration of one quart of spruce beer would weigh), assuming 100% efficiency of the energy to matter transfer, it would take you a mere 90,000,000,000 megawatts to produce that one kilogram of spruce beer. And since by one online source, the entire United States uses about 317,000,000 megawatts per month, it would only take a “mere” 23 years 8 months of all the electric production of the entire United States (as it currently is) to produce enough power to quench your curiosity about what spruce beer tastes like.

Credit: YouTube
Yeah, I don’t see energy-to-matter food replicators happening. Not ever–even if a future society mastered the technology, it seems incredibly wasteful. That’s the kind of thing you’d save for rare engine parts made of out platinum or whatever other very rare mineral. You wouldn’t waste such a technology on food production. Even an advanced food generator that would allow you to replace cooks would make more sense if it used actual matter that’s already around instead of generating it directly from energy. Why not have a kind of advanced digital printer for a replicator instead, that could squirt together food components from a bank of proteins, fats, sugars, starches, and liquids to make your custom food? Much more practical! Though maybe not as tasty…but note that while this sort of technology would allow you to replace field kitchens, it would do nothing to make field rations any smaller.
So any realistic version of a future society will include them needing to pack and supply field rations as much as past ones have done. (In fact, even Star Trek itself at various times references the existence of field rations!)
Of course a story set in a fantasy world can have magical rations. The Lord of the RIngs features Lembas Bread, a bread baked by elves (no, not Keebler elves! 😉 ) that tastes sweet and when in use, one small loaf will provide enough energy for one person for an entire day. The exact weight of a Lembas loaf is unknown, but it does weigh something. Let’s estimate half a pound (227 grams) per Lembas loaf–that means Lembas Bread at maximum is only about 4 times more efficient than freeze-dried food. Though Lembas may have the additional benefit of reducing thirst, note that even an army of elves would have to think about how much Lembas they need versus how much they can carry–and for a long campaign, even magical bread would require wagons of some kind to move it.

Credit: Sorted Food
And of course one would have to consider the resources required to make Lembas or other magical food. Please understand I’m not saying good worldbuilding requires you to calculate all of these things out in every case. But nothing should be free in a story world. Not even magic. You should consider the fact that an army marching to war, even a magical army, will need to plan how it’s going to feed itself when you create your story world. (Of course, spells that generate food from non-food–say rocks into bread–could be one way to solve this issue.)
Food Per Non-Human War Fighter
Ok, we’ve talked about the amount of food a human warrior has needed and various means to supply it. But what if we don’t want to write humans? How much food will a non-human need?
While androids/robots may sustain themselves with mostly energy and a small supply of replacement parts (including replacement hydraulic or lubricating fluid if applicable) and while we can imagine more exotic aliens who perhaps lay out in the sun to gain energy from photosynthesis or magical creatures who derive energy from proximity to crystals or similar notions, these kinds of creatures will be the exception in most stories.Because most inhabitants of speculative fiction stories will need to eat food, just like we do. And while some aliens/magical creatures might be able to consume food humans would get no nutritional value out of, it’s generally useful to think of these beings as eating food the way we do, but needing different amounts.
There are two basic factors that influence how much food a creature needs to survive. The first is metabolic rate, i.e. how much a creature burns per hour at rest. The second is size, with larger creatures needing more food in general than small ones. With the important caveat that larger creatures almost always have lower metabolic rates than smaller ones, so while an elephant may need much more food than a mouse, each bit of tissue in the mouse is actually using far more energy per period of time than the same amount of elephant tissue. While it is true that an elephant eats much more food than a mouse, in proportion to its weight, a mouse burns more calories in proportion to its body weight than an elephant, nearly 12 times as much. So however many mice it would take to weigh as much as an elephant, that number would eat far more than an elephant does!
As explained in an article by Khan Academy, our planet has two kinds of creatures, endothermic (they produce their own heat) and ectothermic (their body temperature matches their surroundings). Birds and mammals are endotherms and pretty much everything else is an ectotherm (note most but not all dinosaurs are now considered to have been endotherms).

Lizardmen vs. Chaos. Credit: Warhammer Wiki
Ectotherms: A pure ectotherm’s metabolism is defined as a Standard Metabolic Rate (SMR)–and the thing is that this rate changes with temperature. So the SMR of any cold-blooded (ectothermic) creature is like an algebraic variable that has a different range for every species–a range and not a fixed value. When it’s colder outside an ectotherm moves slower and uses less calories. When it’s warmer, an ectotherm moves faster and uses more calories. Since an ectotherm is not using its own energy to raise or lower its internal body temperature, it uses much less energy overall than an endotherm, at times as little as 10% of an endotherm’s energy needs. So your army of lizard men can probably skip their breakfast…and carry far fewer supplies…but they are gonna march super slooooow in the morning…though they might get hungry in the afternoon after a quicker pace marching in warm sunlight.
Since the baseline food consumption of an ectotherm is a variable by temperature (not to mention activity), it will be difficult to account for it fully in this post. To provide some means to account for the effect of size alone on ectotherm metabolism, I’ll make reference to an academic paper that says the relationship of size of crocodiles to its SMR is SMR = 1.01 M^0.829 at the standard temperature of 30°C (86°F) (where M=equals weight in kilograms). For many readers this equation will not be meaningful. The following diagram will be better:
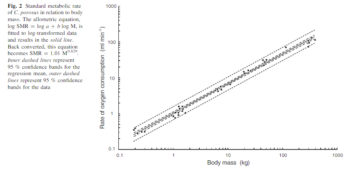
An unfortunate thing about this chart is it measures metabolism in oxygen consumption per minute. It’s possible to convert that to calories but the conversion factor itself is, in truth, a variable. But about 5 calories (we’re talking “calories” as the term is discussed with food and diet, which are actually “kilocalories” in scientific talk) equal one liter of oxygen consumed. But a really big crocodile weighing around 300 kg / 660 lb. uses about 1/10 liter of oxygen in a minute. Which means in ten minutes it burns 1 liter or uses 5 calories energy or 30 cal per hour. That means in a day, doing absolutely nothing, a big (300 kg) crocodile needs 720 calories to stay alive (at 30 degrees C). Since it can get that much from around 300 grams of meat (10.5 ounces), the food needs of any ectotherm/reptilian are very, very low as long as they aren’t doing anything (and are significantly lower when it’s colder outside!).
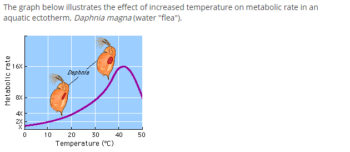
To get a handle on how much temperature affects ectotherm metabolism, let me include a chart from The Biology Place. The chart applies to a specific organism, but shows the general trend for ectotherms to use more energy with higher temperature up to a certain point, above which high temperature causes the ectotherm to begin to shut down–and need to cool off. Note that at 40°C (104°F) an ectotherm uses twice as much resting energy as at 30 C (86°F), but that at 10°C (50°F) it uses only 25% of the energy at 30°C…so our crocodile from above only needs about a measly 180 calories per day to stay alive at 10 C/50 F. This probably would also be true for reptilian humanoids, if such a thing were to actually exist. They can’t warm themselves, but their need for food when their activity is minimal is very, very low! (Of course, when actively moving over an extended period, they need to eat much more.)
Endotherms: Calculating the food needs of an endotherm is actually somewhat easier. An endotherm has a Basal Metabolic Rate (BMR) that reflects the basic amount of energy it needs to regulate its body temperature. That means, laying around, doing nothing, an endotherm burns a certain minimum amount of calories just to stay warm. That number of calories can be thought of as a fixed minimum number per species, though it increases per muscle mass of an individual (which is why human men, who usually have more muscle mass than women, burn more calories per day).
Note that while this post will not provide a specific formula to track it, it’s true that the BMR is higher for creatures prone to heat loss by living in a cold climate (including humans needing more calories in a cold zone than a warm one). As one scholarly article said, “All other things being equal, a polar mammal living at −10°C has a body temperature ∼2·7°C warmer and a BMR higher by ∼40% than a tropical mammal of similar size living at 25°C.” Polar land animals would have to eat 40% more (in their environment).
Likewise, you may not realize it, but living in water causes sea mammals to lose heat much faster than land mammals. While fat under the skin helps slow their heat loss, the BMR of any given sea mammal is much higher than a land mammal of the same size. One study showed at least some species of dolphins weighing around 1oo kg/220 lbs to use about 1 liter per minute of oxygen when resting. Since there are 1,440 minutes in a day, times our rough conversion factor of 1 liter of breathed O2 equaling 5 calories, that means a dolphin of that size (100 kg) and species needs 7,200 calories per day just to stay warm–ten times as much food as a 300 kg crocodile at 30 degrees C. Note a 100 kg human male at rest uses about 2,500 calories a day–a dolphin of the same size to stay warm in water uses nearly three times as much energy and so needs to eat three times as much food. (Merpeople would need to eat a lot!)

Credit: D’nalsi Wiki
While scientific studies note a relationship between a creature’s internal body temperature and its base metabolism–a higher body temperature indicates a higher metabolism–usually this factor is something scientists ignore. They often calculate typical BMR based on the mass of a creature alone, as this generally accounts for observed caloric intake needs. Roughly speaking, though there are variations among orders of mammals and birds (the most important variation being sea mammals and extreme cold weather mammals as already noted, but it’s also true that creatures with bigger brains burn more calories at rest than smaller animals), it’s generally true that the BMR = M^0.75 (where mass equals weight in kilograms–for small mammals and birds this number is more like BMR = M^0.67).
What that math relationship looks like on a chart I’ll show you from an article taken from the Journal of Experimental Biology: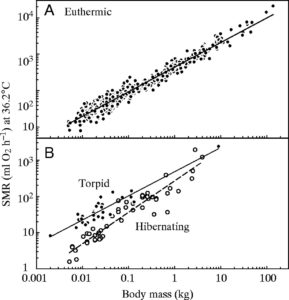 Note that the bottom of the chart tracks mammals while hibernating or “torpid”–i.e. many mammals can enter a state where their metabolic rate plunges and they use far less calories than normal (when they are “entheric,” as the chart puts it).
Note that the bottom of the chart tracks mammals while hibernating or “torpid”–i.e. many mammals can enter a state where their metabolic rate plunges and they use far less calories than normal (when they are “entheric,” as the chart puts it).
An important point to remember on the subject of calculating how much a mammal (or likewise an alien or demi-human) needs to eat is that having to work can greatly increase the amount of calories a living creature will need, beyond the BMR. Human beings rarely double our BMR (the BMR for an average sized American woman is estimated at 1,400 per day and 1,800 for the “average” man), yet for most living creatures who live in the wild, doubling their BMR is the minimum they do on a daily basis. Some animals use up to six times their BMR when active (to give one example, while a dolphin may need roughly 7,000-8,000 calories per day resting, they on average need up to 33,000 calories per day in the wild!) Whether your non-human species typically does between 1.5 and 2 times BMR like a human or 4 to 5 times BMR like a dolphin has to do with how active your species is–if they are using 4 to 5 times as much energy as their BMR, they would pretty much be moving constantly, like dolphins do.
Ok, I’ve given a lot of data here as resources. It may not be immediately clear how to apply this data to world building, but Travis C is going to step in next week to help you put it all together. 🙂
Travis C here. I’ve watched Travis P develop this section through the week, building in detail upon detail of good stuff! Rather than pile on more this week, our next installment will work through an example using Travis P’s research and some of my own to show how a story might evolve via each of our Cost of War considerations.
Stay tuned next week as I unpack Lady Katie’s war against the Mad King Crabcakes as she fields a fantasy army!










































Your discussion of milk needs a little tweaking. During colonial times (and probably further back) silver dollars were used to preserve milk since they lacked refrigeration. Putting a silver dollar in can keep milk fresh from 2-10 days longer. Refrigeration will extend that figure.
But how many more contaminants would a dirty silver dollar introduce?
I didn’t know that, thank you. But I happen to know for certain colonial troops were desperately short of silver!
Instead of energy-to-food replicators, what about something more like 3D printing food? You have a supply of proteins, carbs, fats, flavor-type chemicals, etc, that get assembled into a synthetic food? No idea about the texture and palatability, but something something pun about flavor text.
Also, I still wish somebody would remake Voyager. Neelix and his kitchen was a good idea, but I want less Neelix in general.
I already mentioned printers…look for it. 🙂
I did as you suggested and paid most attention to the bolded print while skimming.
I left some treasures for non-skimmers, too. 🙂
I really enjoyed this post. It had a lot of concrete and useful information. I knew that cold blooded animals burn less energy, for instance, but I didn’t have much of a concrete reference of exactly how much until now. 🙂
Trying to feed an army full of obligate carnivores would be fun. Especially if they were large. Though exactly how that would turn out would depend on different factors. Some carnivores have teeth that are structured in a way that lets them break large bones and get at the marrow, so they would be making the most out of each carcass. Of course, after a battle, they might be able to snack on the carcasses of the opposing side, too, so that might cut down on some of the difficulty.
One thing about keeping herds of prey species is that they can convert unedible things(like weeds we can’t eat) into edible things(meat). From what I understand, goats can eat a lot of things we can’t, and are often used to clear brush from areas that are hard to get to. Since goats are more nimble, can eat a lot of things we can’t, and can also give milk, maybe they would be a good choice for some armies.
Yep, goats would be great in some places. There are some herder tribes in East Africa that have mainly relied on goats (names elude me at the moment, but I’ve actually met such people in Djibouti).
Oh I remember the name now! The Afar people! (Yes, I know it sounds like a fantasy world race, but it isn’t.)
Also, if you have either ancient or modern armies rucking (I.e. marching while carrying 40+ lbs on their back) for hours, they will be burning 4000 – 5000 calories a day. Marching is a lot of work!
German Army figures were lower than that (and German infantry did a lot of marching) and the US Army provides less than that as well for people marching long miles in tough training environments (the Army gives just short of 4000 calories a day). I had heard the 4000-5000 calorie figure before though and was surprised my research pointed to less than that. It’s swimming that burns the most calories for a human!
But I’ll double check my figures. 🙂
Terrain would make a huge difference, though. Plodding up and down sand dunes in the middle of the day is way worse than it would be in a flat, cool meadow.
A 200 lb. man doing an infantry standard ruck march (4 mph) will burn about 450 calories an hour. Add 40 lbs of gear and you burn around 550-600 calories an hour. But it’s probably more calories because historically most soldiers were carrying around 80 lbs of gear and were often required to march much faster. There are reports of men dropping where they stood after long marches and even some cases of men who dropped dead!
I think though that lean, in shape soldiers burn less calories per hour on the march than average people–their bodies get more efficient in processing food over time. The figures from the Colonial and German armies are real figures that were actually used to feed human beings in war time (and for both armies, marching long distances for combat troops was routine).
What’s your source for the 450 calories per hour per 200 lb. man? (I’d like to compare it to the historic data I’ve already seen.)
I used some online calorie calculators. It’s true the more in shape you are would probably be more efficient. I think that the historical figures are correct. Armies don’t march all the time. It seems from many of the accounts I’ve read there is a lot of sitting in camp doing nothing. Or just standing guard. A few days of doing nothing combined with a few days of marching and the calories probably even out.